Máquinas de Moore

1. Máquinas de Estado

 1.2. Máquina de Moore

Uma máquina de Moore é uma maquina de estado finito onde as saídas são determinadas pelo estado corrente presente nas saídas dos flip-flops, ou seja, as saídas só variam quando as saídas dos flip-flops variarem, que acontece somente a cada pulso de clock ( seja na borda de subida ou na borda de descida), tornando-a assim uma máquina cujas saídas são sincronizadas com o clock. O diagrama de estado para uma máquina de Moore não inclui um sinal de saída para cada estado. 

• Transições não possuem uma ação de saída;
• Uma ação de saída está associada a um estado, que neste caso é ativo. O estado produz a ação de saída;
• Cada par único ação/saída é representado através de um estado;
• Utilizado para representar estados observáveis eternamente;
• Produz modelos maiores que o de Mealy;
• Um exemplo de sua aplicação são analizadores léxicos de compiladores ou tradutores de linguagens em geral.

Exemplo de gráfico de estados:

Tabela de Estados

• Obtida diretamente do gráfico de estados

Ex:

Atribuição de Estados

Entrada X0	Estado Presente Q1n Q0n	Saída Z0	Próximo Estado Q1n+1 Q0n+1
0	0    0	0	0        0
0	0    1	0	0       0
0	1    0	0	0      0
0	1    1	1	0      0
1	0    0	0	0      1
1	0    1	0	1      0
1	1    0	0	1      1
1	1    1	1	1      1

Entrada X0	Estado Presente Q1n Q0n	Próximo Estado Q1n+1 Q0n+1	Flip-Flop 1 J1K1	Flip-Flop 0 J0K0	Saída Z0
0	0    0	0        0	0  X	0  X	0
0	0    1	0       0	0  X	X  1	0
0	1    0	0      0	X  1	0  X	0
0	1    1	0      0	X  1	X  1	1
1	0    0	0      1	0  X	1  X	0
1	0    1	1      0	1  X	X  1	0
1	1    0	1      1	X  0	1  X	0
1	1    1	1      1	X  0	X  0	1

Circuito pronto após a análise do mapa de karnout:

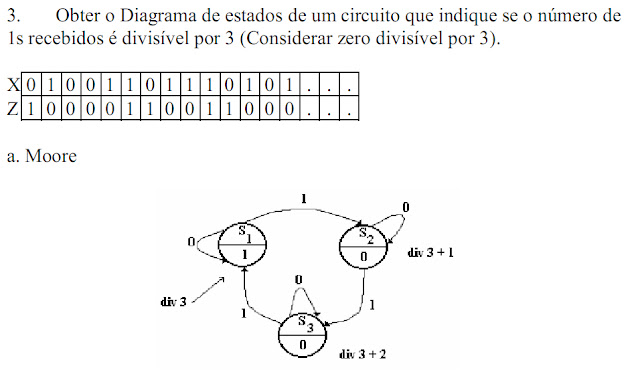
Mais uns exemplos: